CTET November 2012 Mathematics Question Paper (Class I to V).
CTET November 2012 Mathematics Question Paper (Class I to V).
Central Teacher Eligibility Test CTET November 2012 Mathematics Question Paper (Class I to V) Paper I CET Nov 2012 Mathematics Question Paper Answers in Hindi and English Language
Di’rections : Answer the following questions by selecting the most appropriate option.
31. The sum of place values of 2 in 2424 is
(1) 4
(2) 220
(3) 2OO2
(4) 2020
32. (Smallest common multiple of 12 and 16) x (Smallest common multiple of 10 and 15) is equal to
(1) 960
(2) 720
(3) 1440
(4) 480
What should be added to the product 140 * 101 to get 14414?
(1) 264
(2) 274
(3) 278
(4) 364
The sum of all the factors of 100 is
(1) 115
(2) 216
(3) 217
(4) 223
Number of hours and minutes from 6: 14 a.m. to 8 : 02 p.m. on the same day is
(1) 2 hours and 12 minutes
(2) 12 hours and 16 minutes
(3) 13 hours and 48 minutes
(4) 14 hours and 16 minutes
How many 1/6 are there in 3/2
(1) 2
(2) 3
(3) 4
(4) 6
When 121012 is divided by 12, the remainder
(1) 0
(2) 2
(3) 3
(4) 4
Which one of the following is not correct?
(1) 1 paisa = $0.01
(2) one and a half dozen = 18
(3) 1 millimetre = 01 centimetre
(4) 3 litres 30 millilitres = 330 millilitres
A chocolate has 12 equal pieces. Manju gave one-fourth of it to Anju, one-third of it to Sujatha and one-sixth of it to Fiza. The number of pieces of chocolate left with Manju
(1) 1
(2) 2
(3) 3
(4) 4
One orange costs two and a half rupees. How much will three and a half dozen oranges cost?
(1) Rs. 90
(2) Rs. 105
(3) Rs. 112
(4) Rs. 120
Floor of a square room of side 10 metres is to be completely covered with square tiles, each having length 50 centimetres. The smallest number of tiles needed is
(1) 200
(2) 300
(3) 400
(4) 500
The perimeter of two squares is 12 cm and 24 cm. The area of the bigger square is how many times that of the smaller?
(1) 2 times
(2) 3 times
(3) 4 times
(4) 5 times
Internal length, breadth and height of a rectangular box are 10 cm, 8 cm and 6 cm respectively. How many boxes are needed to pack 6240 centimetre cubes?
(1) 12
(2) 13
(3) 15
(4) 17
The number of degrees in four and one-third right angles is
(1) 390
(2) 395
(3) 400
(4) 405
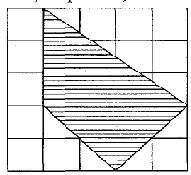
In the figure, side of each square is 1 cm. The area, in square cm, of the shaded part is
(1) 8
(2) 9
(3) 10-
(4).11
Shailja can express a number in different ways. For example 4 =2 + 2 or 4 = 1 + 3 etc. In which developmental phase of numbers is she?
(1) Quantifying phase
(2) Partitioning phase
(3) Factoring phase
(4) Operating phase
A child of Class III reads 482 as four hundred eighty two but writes it as 40082. What does this indicate for a teacher?
(1) Child is not attentive in the class and is a careless listener
(2) Child is a careful listener but has not established sense of place value
(3) Child is confusing the expression of number in expanded form and in short form
(4) Teacher should teach the concept of place value when the children are able to write numbers correctly
To introduce subtraction of two-digit numbers in Class• 111, a teacher proceeded in the following steps:
Step I: Revision of two-digit numbers with understanding of place value system..
Step II: Use of tally marks to show that smaller number can be subtracted from larger number.
Step III Application of subtraction on numbers under each column of place value.
In this case teacher is developing the lesson
(1) from system concept —* operation algorithm
(2) from operation —+ system concept algorithm
(3) from algorithm — system concept operation
(4) from system concept —* algorithm operation
“Which two numbers when multiplied give the product 24 ?“ This question
(1) is an open ended question as it has more than one answer
(2) is a closed-ended question as it has) definite number of answers
(3) suggests general problem-solving strategy to the child so that he/she can answer correctly
(4) helps the child to think metacognitively
The students of Class V were able to attempt the problem 1/2 ÷ 1/3 correctly, but not able to solve the problem ‘How many 1/3 cake pieces are there in half a cake ?“. The reason is
(1) students’ language development is poor
(2) problem is of higher difficulty level for Class V
(3) operations on fractions are taught without contextualization and language support
(4) students are not able to understand the mathematical equivalence of the two problems
Hamida always allow her students to observe the number pattern and to form conjectures on their own in order to enhance their mathemical abilities. She wrote the followin problems on board and asked the students to write the answers:
21÷7=
2.1÷0.7=
0.21 ÷ 0.07 =
0.021 ÷ 0.007 =
Through the set of questions she wants the students to observe that
(1) as one factor is divided by 10 and the other is multiplied by 10, the product remains same
(2) as one divisor is decreased by 10 and the other is increased by power of 10, the product remains same
(3) if both the divisor and the dividend are increased or decreased by power of 10, the quotient remains the same
(4) if both the divisor and the dividend are decreased by power of 10, the quotient is also decreased by the power of 10
Piaget believed that learning results from social instruction and a mathematics teacher believing in Piaget’s theory shall use
(1) lots of manipulatives and lab activities in the class
(2) group project and group discussion
(3) differentiated instruction
(4) chalk and talk method
Pradeep was shown a broken ruler
![]()
and asked, where is 5 cm on the ruler. He picked up the ruler and pointed at the mark of 5 cm on the ruler. His answer
(1) is correct as he rightly pointed out the mark of 5 cm on the ruler
(2) is incorrect as he is showing a point only and not the distance between two points marked as 0 and 5
(3) is incorrect as the ruler is broken and he must start with 2 and should point at 7 as the desired mark
(4) is reflecting that he has the misconception that 5 cm refers to a point and not to a length
Uma was not able to understand the concept of odd and even numbers. In order to improve her understanding, the teacher took some 20 pebbles of different colours and asked her to pair them up and sort out the numbers from 1 to 20 for which pebbles get paired up or do not get paired up. Uma
(1) is a visual learner
(2) is a kinesthetic learner
(3) is an auditory learner
(4) needs personal attention
Rubrics of assessment for the geometry lesson on points and lines in Class IV shall be
(1) can differentiate between line and line segment, can mark a point, can draw a line segment of given length accurately
(2) can measure the line in cms and inches accurate’y, can name the line
(3) can measure the line segment in cms and inches accurately and can mark end points of line segment
(4) can differentiate between line, ray and line segment and can define them
In a class, a teacher asked the students to define a quadrilateral in different ways — using sides, using angles, using diagonals etc. The teacher’s objective is to
(1) help the students to explore various definitions
(2) help the students to understand quadrilateral from different perspectives
(3) help the students to memorize all definitions by heart
(4) help the students to solve all problems of quadrilateral based on definitions
Students arc asked to establish a relation between vertically opposite angles. They draw ‘various figures, measure the angles and observe that vertically opposite angles are equal. In this case, students according to Van Hide
thought are at
(1) Visualization level
(2) Analytic level
(3) Informal Deduction level
(4) Deduction level
Higher Order Thinking Skills (HOTS) based questions demand the
(1) knowledge of facts, rules, formulae
(2) knowledge of algorithm
(3) knowledge of symbols and diagrams
(4) knowledge and some degree of cognitive efforts
Most appropriate formative task to assess the students’ understanding of data analysis is
(1) Quiz
(2) Role play
(3) Crossword
(4) Survey-based Project
Classroom discussion was initiated in Class V on ‘Sale’ in festival season, during topic of ‘Percentage’. This type of discussion in classroom
(1) helps the students to listen to each other’s opinion and encourages them to present their argument
(2) must be avoided as it raises the noise level of class and disturbs others
(3) helps the students to enhance their debating skills
(4) starts heated arguments in class and spoils the atmosphere of the class
Similar Pages….
See Also……